Analysis of Short Time Series
Posted onI enjoy reading Rob Hyndman’s blog. The other day he did some analysis of a short times series. More about that is available at his blog here. The neat thing that he shows is that you don’t need a tremendous amount of data to decompose seasonality. Using fourier transforms1.
He sets up a small data set:
df <-
Which only has 20 months of data in it. He then applies a time series linear model with 2 sine/ cosine pair terms.
decompose_df <-
We can see the coefficients of the model here:
Call:
tslm(formula = df ~ trend + fourier(df, 2))
Residuals:
Min 1Q Median 3Q Max
-100.572 -33.513 5.743 24.430 79.728
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2637.357 24.862 106.080 < 2e-16 ***
trend 24.541 2.077 11.816 1.14e-08 ***
fourier(df, 2)S1-12 76.553 17.105 4.475 0.000523 ***
fourier(df, 2)C1-12 -4.281 17.105 -0.250 0.806010
fourier(df, 2)S2-12 36.931 16.203 2.279 0.038850 *
fourier(df, 2)C2-12 10.402 16.802 0.619 0.545780
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 50.98 on 14 degrees of freedom
Multiple R-squared: 0.917, Adjusted R-squared: 0.8874
F-statistic: 30.94 on 5 and 14 DF, p-value: 4.307e-07
From there tou can see the trends for each of the components.
trend <- + *
components <-
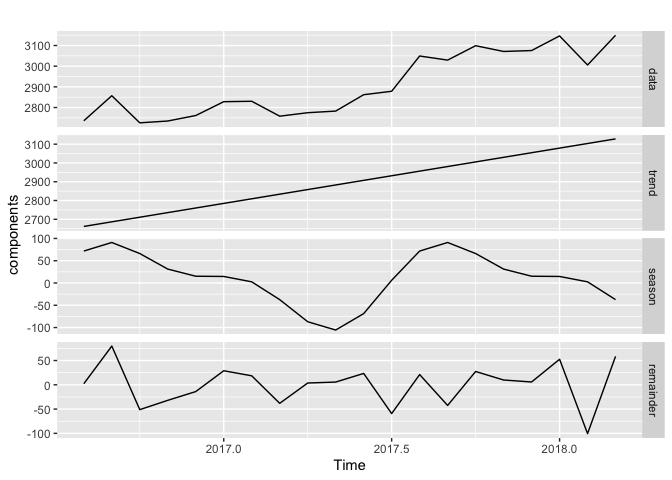
out <-
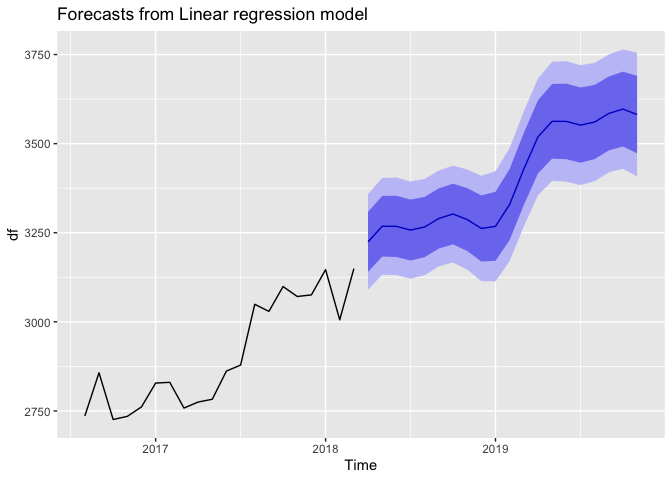
Citation
BibTex citation:
@online{dewitt2018
author = {Michael E. DeWitt},
title = {Analysis of Short Time Series},
date = 2018-07-19,
url = {https://michaeldewittjr.com/articles/2018-07-19-analysis-of-short-time-series},
langid = {en}
}
For attribution, please cite this work as:
Michael E. DeWitt. 2018. "Analysis of Short Time Series." July 19, 2018. https://michaeldewittjr.com/articles/2018-07-19-analysis-of-short-time-series