a foray into network analysis

Posted on

Marriage Networks of Florence

This post takes the example provided in Kosuke Imai’s Quantitative Social Science: An Introduction. It provides some exploration of network analysis through looking at the florentine dataset which counts the marraige relationships between several Florentine families in the 15th century. My historical side knows that our analysis should show that the [Medici Family] should appear at the center of all of the political intrigue. Let’s see if the analysis plays out.

Formatting the Data

The florentine data set comes as a dataframe. In order to work with igraph it will need to be converted to a matrix with named columns and rows. That conversion can be done here:

Starting Table

FAMILY ACCIAIUOL ALBIZZI BARBADORI BISCHERI
ACCIAIUOL 0 0 0 0
ALBIZZI 0 0 0 0
BARBADORI 0 0 0 0
BISCHERI 0 0 0 0
CASTELLAN 0 0 1 0
GINORI 0 1 0 0
GUADAGNI 0 1 0 1
LAMBERTES 0 0 0 0
MEDICI 1 1 1 0
PAZZI 0 0 0 0
PERUZZI 0 0 0 1
PUCCI 0 0 0 0
RIDOLFI 0 0 0 0
SALVIATI 0 0 0 0
STROZZI 0 0 0 1
TORNABUON 0 0 0 0

Now we need to manipulate the dataframe to turn it into a matrix object so that we can pass it to the igraph package.

florentine_g <- florentine %>%
  filter(FAMILY != "PUCCI") %>%
  select(-PUCCI) %>%
  select(-FAMILY) %>%
  as.matrix()

row.names(florentine_g) <- florentine[-12,1] %>% as.vector()

Now we need to pass this object to igraph. The path is undirected because there is no ordinality to this data. It does not encode if one family proposed the marriage to the other group. If this were the case then there could be some directedness to the graph. In this case there isn’t so that is the parameter we will pass.

florentine_g <- graph.adjacency(florentine_g, mode = "undirected", diag = FALSE)

Now we can plot based on several features:

  • degree

  • closeness

  • betweeness

  • PageRank

Visualising the Network

plot(florentine_g, vertex.size = betweenness(florentine_g), main = "Betweeness")


plot(florentine_g, vertex.size = closeness(florentine_g)*1000, main = "Closeness")


plot(florentine_g, vertex.size = degree(florentine_g)*10, main = "Degree")

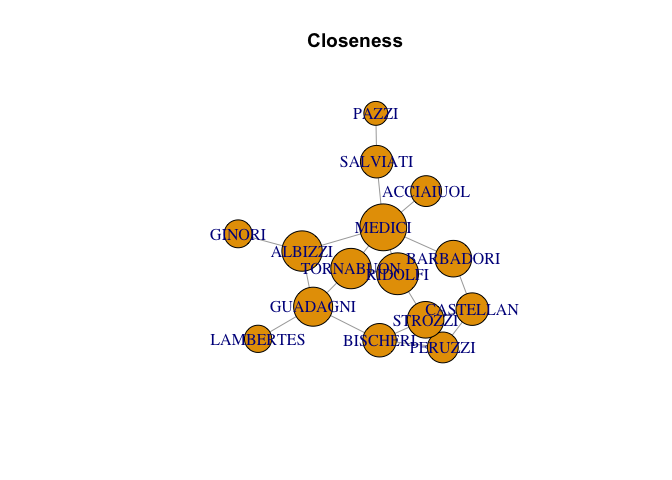
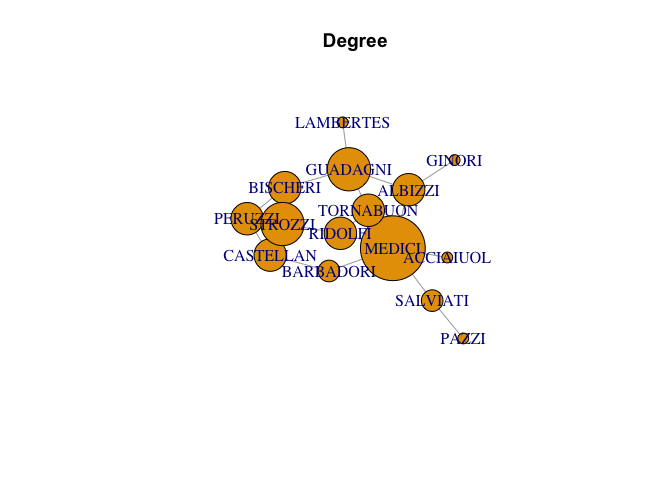
The Numeric Outputs

floretine_networks <- data_frame(
  family = names(closeness(florentine_g)),
  closeness = closeness(florentine_g),
  degree = degree(florentine_g),
  betweeness = betweenness(florentine_g)
) %>%
  arrange(-closeness)

kable(floretine_networks)
family closeness degree betweeness
MEDICI 0.0400000 6 47.500000
RIDOLFI 0.0357143 3 10.333333
ALBIZZI 0.0344828 3 19.333333
TORNABUON 0.0344828 3 8.333333
GUADAGNI 0.0333333 4 23.166667
BARBADORI 0.0312500 2 8.500000
STROZZI 0.0312500 4 9.333333
BISCHERI 0.0285714 3 9.500000
CASTELLAN 0.0277778 3 5.000000
SALVIATI 0.0277778 2 13.000000
ACCIAIUOL 0.0263158 1 0.000000
PERUZZI 0.0263158 3 2.000000
GINORI 0.0238095 1 0.000000
LAMBERTES 0.0232558 1 0.000000
PAZZI 0.0204082 1 0.000000

Additionally, the “pagerank” algorithm can be used.

plot(florentine_g, vertex.size = page.rank(graph = florentine_g, directed = FALSE)$vector*100)


Citation

BibTex citation:

@online{dewitt2018
author = {Michael E. DeWitt},
title = {a foray into network analysis},
date = 2018-09-17,
url = {https://michaeldewittjr.com/articles/2018-09-16-a-foray-into-network-analysis},
langid = {en}
}

For attribution, please cite this work as:

Michael E. DeWitt. 2018. "a foray into network analysis." September 17, 2018. https://michaeldewittjr.com/articles/2018-09-16-a-foray-into-network-analysis