Replicating gsynth

Posted on

Introduction

Synthethic methods are a method of causal inference that seeks to combine traditional difference-in-difference types studies with time series cross sectional differences with factor analysis for uncontrolled/ unobserved measures. This method has been growing our of work initially from Abadie (Abadie, Diamond, and Hainmueller 2011a) and growing in importance/ research for state level policy analysis. It is interesting from the fact that it combines some elements of factor analysis to develop predictors and regression analysis to try to capture explained and unexplained variance.

Package

library(tidyverse)
library(gsynth)
library(panelView)

Method Assumptions

This methodology makes several critical assumptions.

  1. The model takes the functional form of Yi,t=δi,tDi,t+xi,t<sup>′β+λi</sup>′fi+ϵi,tY_{i,t}=\delta_{i,t}D_{i,t}+x_{i,t}<sup>\prime\beta+\lambda_i</sup>{\prime}f_i+\epsilon_{i,t}
  2. Strict exogeneity (e.g. the error terms are indepdent to D, X, λ\lambda and f)
  3. Weak serial dependence of the error terms
  4. Regularity of conditions

The method then uses bootstrapping for confidence intervals.

There is some basic data available in the package

data(gsynth)

The data that will be initially used will be the simdata dataset

id time Y D X1 X2 eff error mu alpha xi F1 L1 F2 L2
116 1 4.96 0 0.75 0.23 0.00 -2.60 5 -0.36 1.13 0.25 1.39 0.01 -0.18
114 29 16.90 0 0.87 2.83 8.96 0.50 5 -1.53 3.24 0.18 0.25 -0.38 -0.78
101 10 1.44 0 1.52 -0.55 0.00 -0.74 5 -0.06 -1.60 0.22 -0.04 1.15 -0.88
125 6 15.78 0 2.20 2.91 0.00 -0.99 5 -0.65 0.70 1.52 0.54 0.33 -0.09
129 11 9.63 0 0.14 1.34 0.00 0.19 5 1.62 -0.53 0.38 -0.73 0.99 -0.51
101 12 5.47 0 1.43 0.33 0.00 0.04 5 -0.06 -1.46 -0.50 -0.04 0.55 -0.88
119 9 10.94 0 2.65 2.17 0.00 -0.09 5 -1.20 -1.51 0.12 -0.60 -0.33 1.02
134 18 13.71 0 1.72 2.28 0.00 -0.96 5 -0.81 0.33 0.05 1.02 1.53 1.00
140 4 7.83 0 2.38 -0.18 0.00 -0.21 5 1.28 1.91 1.37 -0.93 0.64 -1.13
133 25 12.05 0 1.08 1.97 3.45 0.30 5 0.32 -0.37 -0.69 0.66 -0.95 -0.29
109 15 17.43 0 2.98 2.98 0.00 -0.56 5 0.69 -1.29 -1.07 0.18 1.36 1.37
104 23 21.17 1 2.60 2.27 3.52 0.07 5 1.34 -0.37 1.01 2.02 -0.25 -0.62
128 30 4.79 0 2.31 -0.50 8.95 -2.55 5 1.63 -0.42 -0.14 0.33 0.92 0.39
119 8 6.02 0 0.83 0.99 0.00 -0.09 5 -1.20 -1.57 0.58 -0.60 0.44 1.02
122 7 8.50 0 0.71 1.23 0.00 -0.66 5 0.56 -0.26 -1.55 0.67 1.10 0.45
122 2 9.68 0 2.00 1.01 0.00 0.39 5 0.56 -1.46 -0.03 0.67 0.39 0.45
104 25 9.31 1 0.39 -0.53 5.33 0.02 5 1.34 -0.37 -0.69 2.02 -0.95 -0.62
109 16 12.81 0 -1.41 2.24 0.00 1.78 5 0.69 0.79 0.30 0.18 -0.60 1.37
143 8 6.43 0 -0.36 0.90 0.00 0.48 5 0.60 -1.57 0.58 -0.30 0.44 -0.54
134 27 2.32 0 -0.13 0.36 8.13 -0.71 5 -0.81 -1.05 -0.28 1.02 -0.78 1.00
125 16 3.00 0 0.66 -0.67 0.00 -1.01 5 -0.65 0.79 0.30 0.54 -0.60 -0.09
130 17 -7.68 0 -0.10 -3.48 0.00 -0.19 5 0.79 0.77 0.45 -1.22 2.19 -1.35
129 10 7.47 0 1.15 0.75 0.00 -0.21 5 1.62 -1.60 0.22 -0.73 1.15 -0.51
132 29 10.77 0 -0.02 1.23 11.04 -0.19 5 -0.96 3.24 0.18 1.39 -0.38 0.58
143 29 13.15 0 2.11 0.24 8.82 1.33 5 0.60 3.24 0.18 -0.30 -0.38 -0.54

It can be examined via the panelView package:

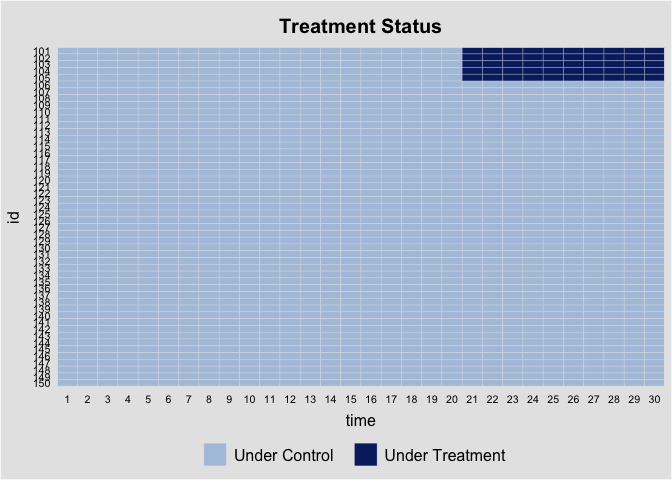
panelview(Y ~ D, data = simdata,  index = c("id","time"))

Modeling

out <- gsynth(Y ~ D + X1 + X2, data = simdata,
                  index = c("id","time"), force = "two-way",
                  CV = TRUE, r = c(0, 5), se = TRUE,
                  inference = "parametric", nboots = 1000,
                  parallel = FALSE)

Cross-validating ...
 r = 0; sigma2 = 1.84865; IC = 1.02023; PC = 1.74458; MSPE = 2.37280
 r = 1; sigma2 = 1.51541; IC = 1.20588; PC = 1.99818; MSPE = 1.71743
 r = 2; sigma2 = 0.99737; IC = 1.16130; PC = 1.69046; MSPE = 1.14540*
 r = 3; sigma2 = 0.94664; IC = 1.47216; PC = 1.96215; MSPE = 1.15032
 r = 4; sigma2 = 0.89411; IC = 1.76745; PC = 2.19241; MSPE = 1.21397
 r = 5; sigma2 = 0.85060; IC = 2.05928; PC = 2.40964; MSPE = 1.23876

 r* = 2


Simulating errors .............
Bootstrapping ...
..........

print(out)

Call:
gsynth.formula(formula = Y ~ D + X1 + X2, data = simdata, index = c("id",
    "time"), force = "two-way", r = c(0, 5), CV = TRUE, se = TRUE,
    nboots = 1000, inference = "parametric", parallel = FALSE)

Average Treatment Effect on the Treated:
        Estimate  S.E. CI.lower CI.upper p.value
ATT.avg    5.544 0.262     5.03    6.057       0

   ~ by Period (including Pre-treatment Periods):
          ATT   S.E. CI.lower CI.upper   p.value n.Treated
-19  0.392160 0.5468  -0.6796  1.46396 4.733e-01         0
-18  0.276548 0.4461  -0.5979  1.15098 5.354e-01         0
-17 -0.275393 0.5428  -1.3392  0.78841 6.119e-01         0
-16  0.441201 0.4389  -0.4191  1.30150 3.148e-01         0
-15 -0.889595 0.4914  -1.8527  0.07348 7.023e-02         0
-14  0.593891 0.4633  -0.3142  1.50199 1.999e-01         0
-13  0.528749 0.4132  -0.2811  1.33860 2.007e-01         0
-12  0.171569 0.5975  -0.9994  1.34258 7.740e-01         0
-11  0.610832 0.4474  -0.2661  1.48774 1.722e-01         0
-10  0.170597 0.4516  -0.7146  1.05581 7.056e-01         0
-9  -0.271892 0.5871  -1.4226  0.87886 6.433e-01         0
-8   0.094843 0.5037  -0.8924  1.08204 8.506e-01         0
-7  -0.651976 0.5567  -1.7430  0.43904 2.415e-01         0
-6   0.573686 0.4783  -0.3638  1.51113 2.304e-01         0
-5  -0.469686 0.5150  -1.4792  0.53978 3.618e-01         0
-4  -0.077766 0.5287  -1.1140  0.95850 8.831e-01         0
-3  -0.141785 0.5473  -1.2144  0.93085 7.956e-01         0
-2  -0.157100 0.4186  -0.9776  0.66341 7.075e-01         0
-1  -0.915575 0.4856  -1.8673  0.03616 5.936e-02         0
0   -0.003309 0.3638  -0.7164  0.70975 9.927e-01         0
1    1.235962 0.7289  -0.1927  2.66458 8.995e-02         5
2    1.630264 0.5615   0.5297  2.73079 3.691e-03         5
3    2.712178 0.5508   1.6326  3.79178 8.487e-07         5
4    3.466758 0.7437   2.0092  4.92431 3.136e-06         5
5    5.740132 0.5367   4.6882  6.79203 0.000e+00         5
6    5.280035 0.5741   4.1548  6.40529 0.000e+00         5
7    8.436485 0.4843   7.4874  9.38561 0.000e+00         5
8    7.839902 0.6408   6.5839  9.09592 0.000e+00         5
9    9.455115 0.5450   8.3869 10.52329 0.000e+00         5
10   9.638509 0.5035   8.6517 10.62527 0.000e+00         5

Coefficients for the Covariates:
    beta    S.E. CI.lower CI.upper p.value
X1 1.022 0.03004    0.963    1.081       0
X2 3.053 0.02958    2.995    3.111       0

out$est.att

             ATT      S.E.   CI.lower    CI.upper      p.value n.Treated
-19  0.392159788 0.5468489 -0.6796443  1.46396386 4.732961e-01         0
-18  0.276547958 0.4461493 -0.5978887  1.15098460 5.353532e-01         0
-17 -0.275392926 0.5427657 -1.3391941  0.78840827 6.118824e-01         0
-16  0.441201288 0.4389354 -0.4190963  1.30149888 3.148187e-01         0
-15 -0.889595124 0.4913755 -1.8526735  0.07348322 7.023098e-02         0
-14  0.593890957 0.4633226 -0.3142046  1.50198651 1.999097e-01         0
-13  0.528749012 0.4131945 -0.2810973  1.33859533 2.006643e-01         0
-12  0.171568737 0.5974650 -0.9994412  1.34257868 7.739889e-01         0
-11  0.610832288 0.4474116 -0.2660784  1.48774295 1.721720e-01         0
-10  0.170597468 0.4516495 -0.7146193  1.05581419 7.056379e-01         0
-9  -0.271891657 0.5871305 -1.4226462  0.87886293 6.433030e-01         0
-8   0.094842558 0.5036802 -0.8923526  1.08203768 8.506422e-01         0
-7  -0.651975701 0.5566512 -1.7429921  0.43904067 2.414998e-01         0
-6   0.573686472 0.4782973 -0.3637590  1.51113193 2.303589e-01         0
-5  -0.469685905 0.5150445 -1.4791545  0.53978268 3.618041e-01         0
-4  -0.077766449 0.5287181 -1.1140349  0.95850205 8.830650e-01         0
-3  -0.141784521 0.5472736 -1.2144212  0.93085211 7.955779e-01         0
-2  -0.157100323 0.4186374 -0.9776145  0.66341385 7.074627e-01         0
-1  -0.915575087 0.4855890 -1.8673120  0.03616184 5.936318e-02         0
0   -0.003308833 0.3638145 -0.7163722  0.70975454 9.927435e-01         0
1    1.235962010 0.7289023 -0.1926602  2.66458419 8.995247e-02         5
2    1.630264312 0.5615032  0.5297382  2.73079044 3.691436e-03         5
3    2.712177702 0.5508277  1.6325753  3.79178010 8.486982e-07         5
4    3.466757691 0.7436652  2.0092007  4.92431464 3.135799e-06         5
5    5.740132310 0.5366920  4.6882353  6.79202929 0.000000e+00         5
6    5.280034526 0.5741182  4.1547836  6.40528546 0.000000e+00         5
7    8.436484821 0.4842566  7.4873594  9.38561026 0.000000e+00         5
8    7.839901526 0.6408388  6.5838805  9.09592251 0.000000e+00         5
9    9.455114684 0.5449999  8.3869345 10.52329485 0.000000e+00         5
10   9.638509457 0.5034590  8.6517480 10.62527087 0.000000e+00         5

out$est.avg

        Estimate     S.E. CI.lower CI.upper p.value
ATT.avg 5.543534 0.262005 5.030014 6.057054       0

out$est.beta

       beta       S.E.  CI.lower CI.upper p.value
X1 1.021890 0.03004240 0.9630082 1.080772       0
X2 3.052994 0.02957771 2.9950231 3.110966       0

The default plot:

plot(out) +
  theme(plot.title = element_text(size = 12))

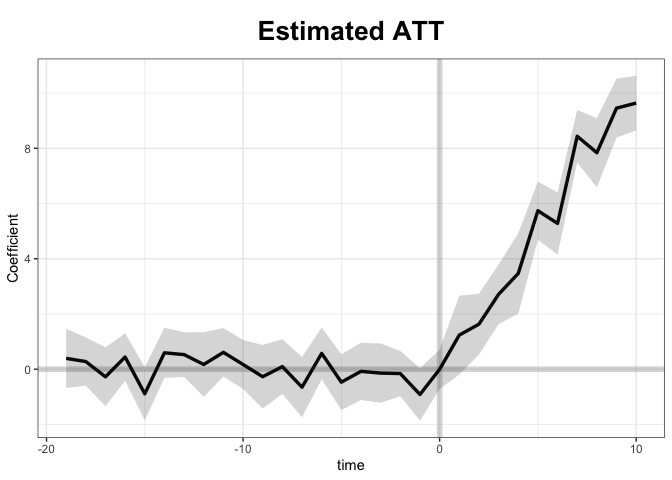
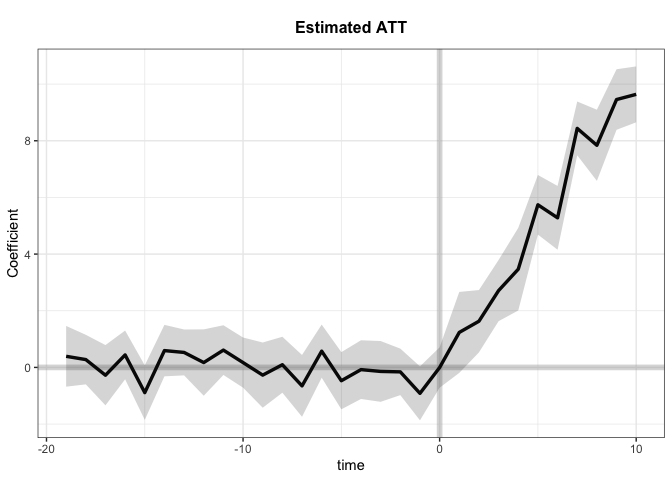
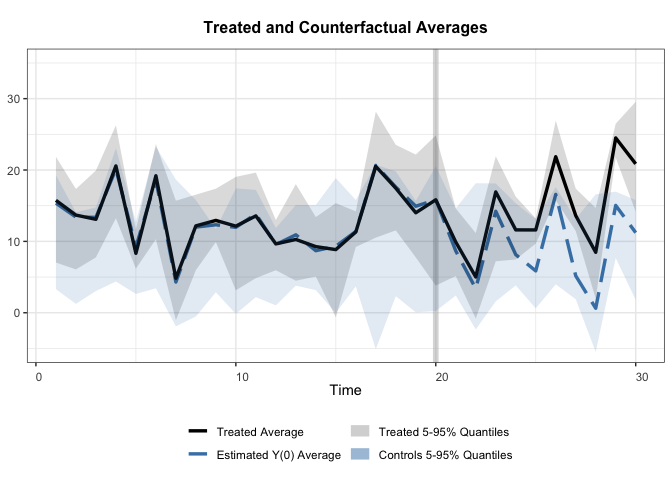
Modified:

plot(out, theme.bw = TRUE) +
  theme(plot.title = element_text(size = 12))

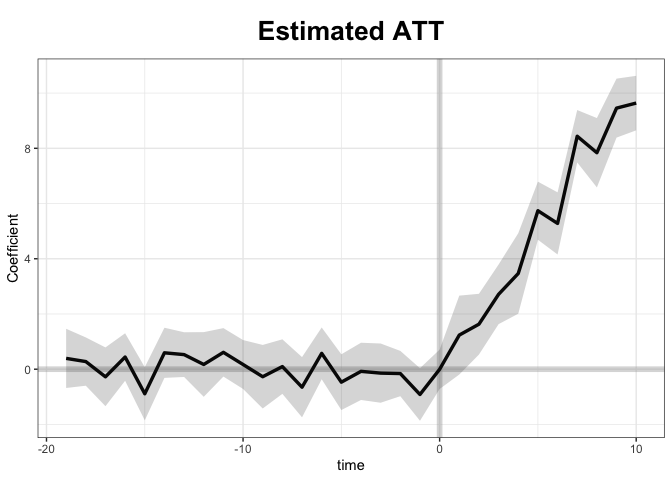
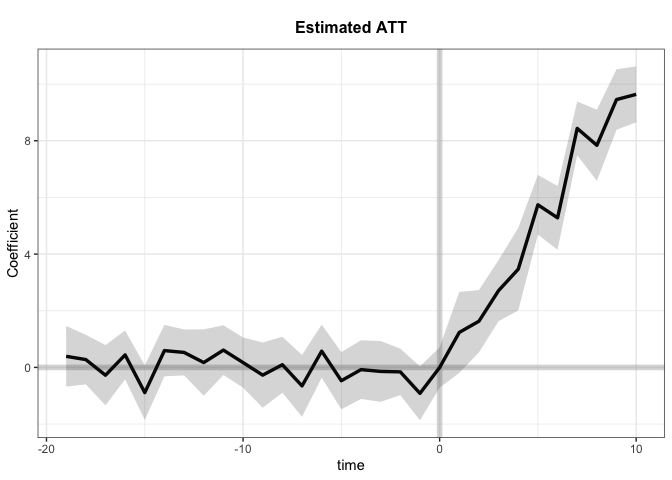
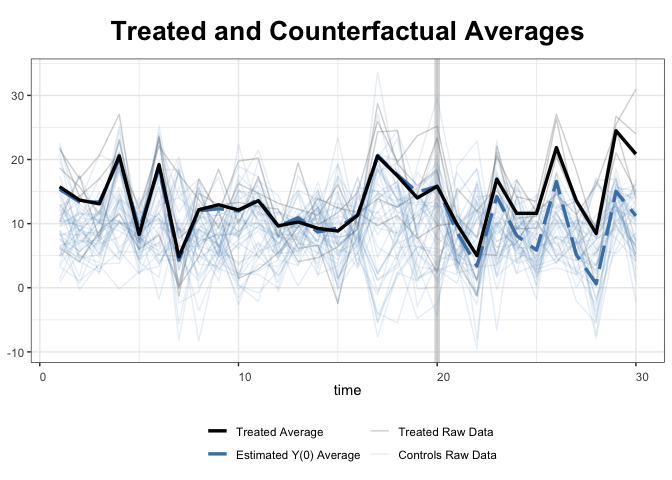
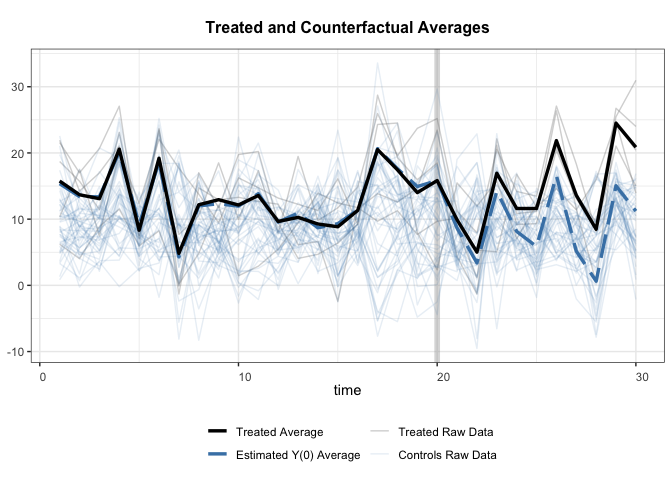
With the raw data:

plot(out, type = "raw", theme.bw = TRUE)+
  theme(plot.title = element_text(size = 12))


plot(out,type = "raw", legendOff = TRUE, ylim=c(-10,40), main="")+
  theme(plot.title = element_text(size = 12))


plot(out, type = "counterfactual", raw = "none", main="")+
  theme(plot.title = element_text(size = 12))


plot(out, type = "counterfactual", raw = "band", xlab = "Time",
     ylim = c(-5,35), theme.bw = TRUE)+
  theme(plot.title = element_text(size = 12))


plot(out, type = "counterfactual", raw = "all")+
  theme(plot.title = element_text(size = 12))


plot(out, type = "factors", xlab = "Time")+
  theme(plot.title = element_text(size = 12))

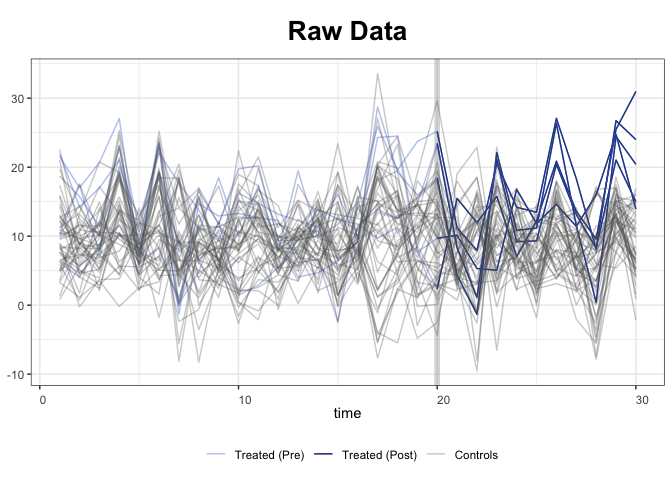
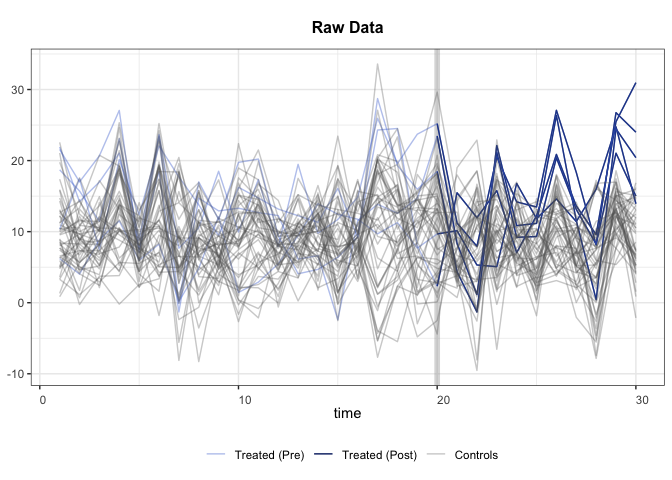
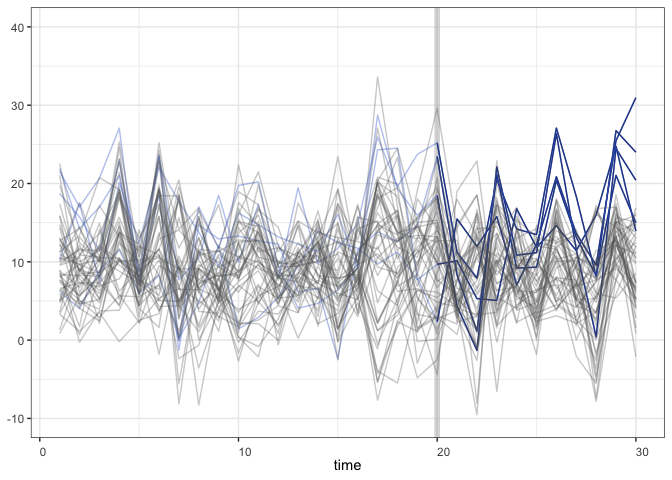
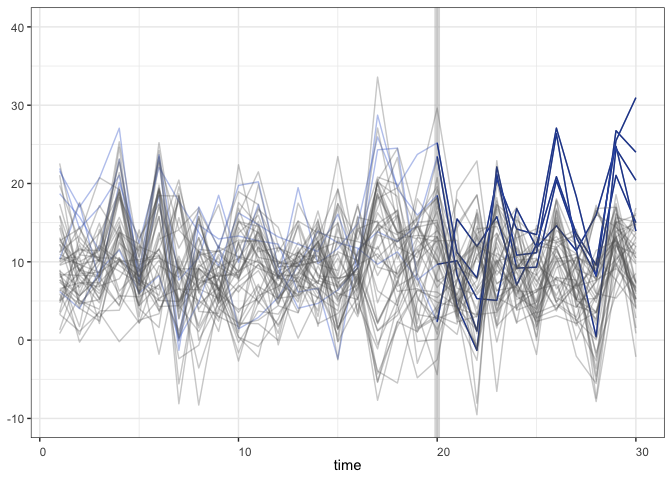
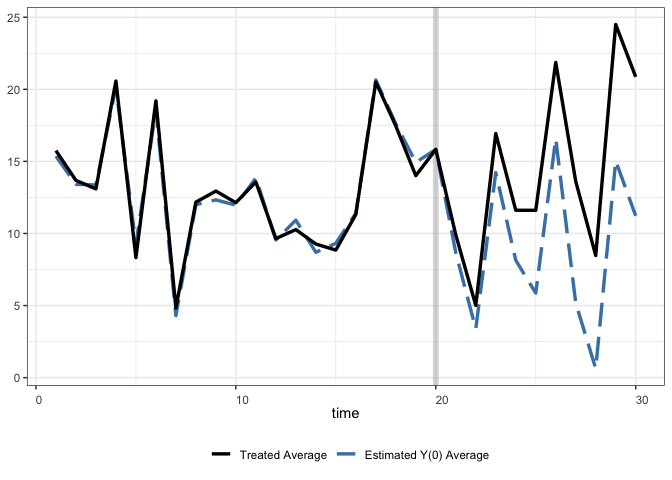
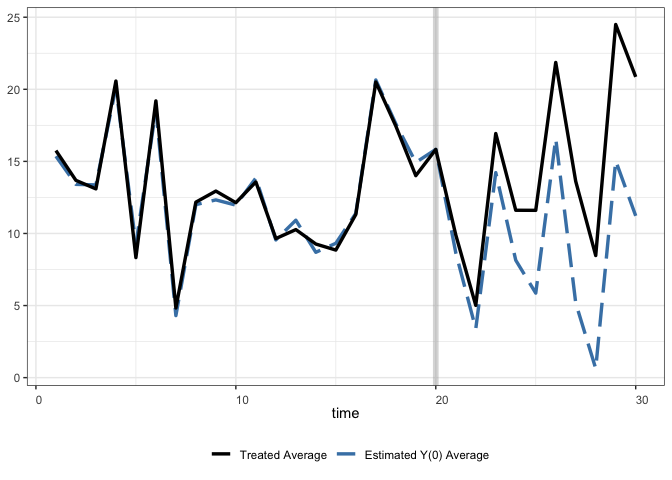
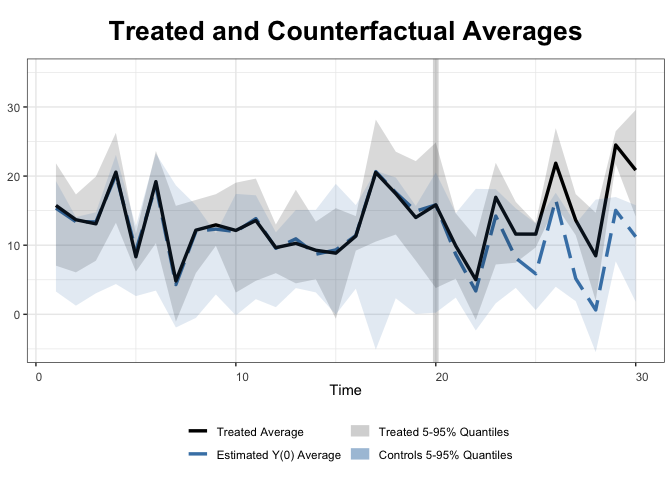
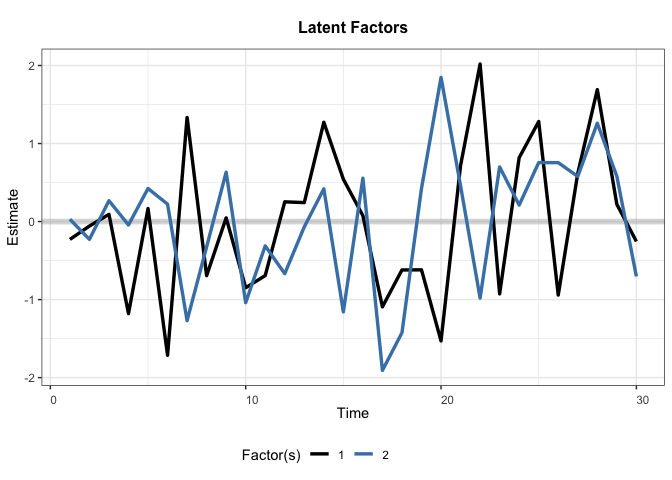
Voter Turnout

Now I am going to try to reproduce the results from Xu’s paper [xu_generalized_2017] and implemented in his package (Xu and Liu 2018).

Data

abb year turnout policy_edr policy_mail_in policy_motor
AL 1920 21.02107 0 0 0
AL 1924 13.58233 0 0 0
AL 1928 19.03850 0 0 0
AL 1932 17.62002 0 0 0
AL 1936 18.69238 0 0 0
AL 1940 18.86406 0 0 0

Model

The paper builds two models, one will only the impact of voter education, another with additional controls. For the sake of time I will build the model with all of the controls used.

out <- gsynth(turnout ~ policy_edr + policy_mail_in + policy_motor, data = turnout,
                  index = c("abb","year"), force = "two-way",
                  CV = TRUE, r = c(0, 5), se = TRUE,
                  inference = "parametric", nboots = 1000,
                  parallel = FALSE)

Cross-validating ...
 r = 0; sigma2 = 77.99366; IC = 4.82744; PC = 72.60594; MSPE = 22.13889
 r = 1; sigma2 = 13.65239; IC = 3.52566; PC = 21.67581; MSPE = 12.03686
 r = 2; sigma2 = 8.56312; IC = 3.48518; PC = 19.23841; MSPE = 10.31254*
 r = 3; sigma2 = 6.40268; IC = 3.60547; PC = 18.61783; MSPE = 11.48390
 r = 4; sigma2 = 4.74273; IC = 3.70145; PC = 16.93707; MSPE = 16.28613
 r = 5; sigma2 = 4.02488; IC = 3.91847; PC = 17.05226; MSPE = 15.78683

 r* = 2


Simulating errors .............
Bootstrapping ...
..........

The model completed and appeared that it did well. Now to examine the figures to see if they match:

plot(out)

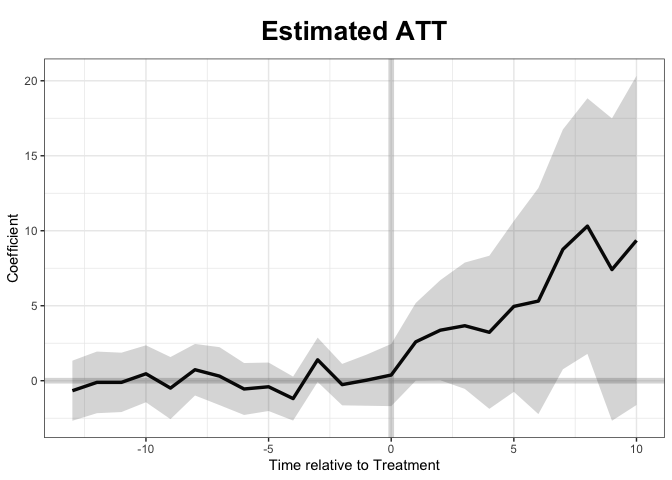
Now we can look at the estimated average treatment

out$est.avg %>%
  knitr::kable()
Estimate S.E. CI.lower CI.upper p.value
ATT.avg 4.895788 2.315232 0.3580163 9.43356 0.0344641 
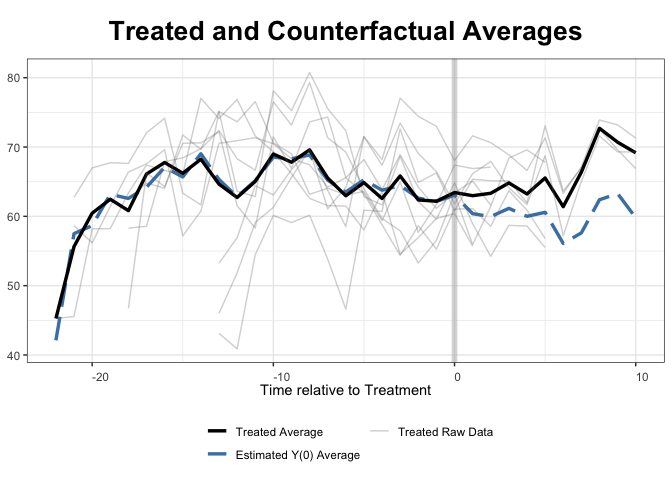
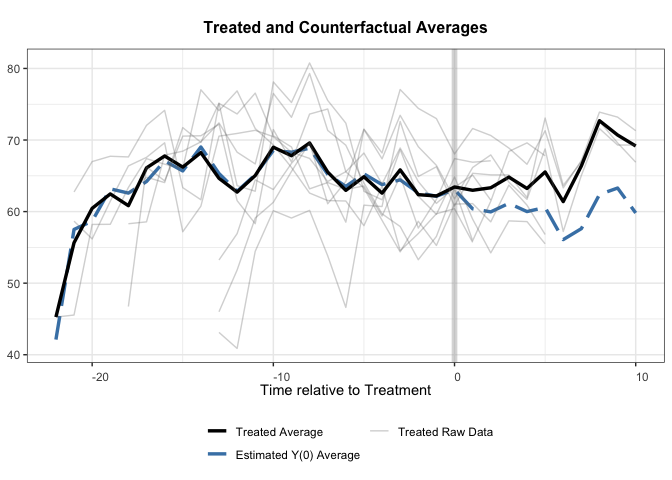
plot(out, type = "counterfactual", raw = "all")+
  theme(plot.title = element_text(size = 12))

Now with Synth

Now I want to try to replicate the previous case study used in Synth (Abadie, Diamond, and Hainmueller 2011b) and see if it is possible.

library(Synth)

I am going to recode some variable in order to fit with the methods used in gsynth. The Synth package uses a dataprep function in order to format the data into the requirements.

data("basque")
basque_treat <- basque %>%
  mutate(treat = ifelse(grepl(pattern = "Basque", x = regionname) & year > 1969,1,0))
head(basque_treat) %>%
  knitr::kable()
regionno regionname year gdpcap sec.agriculture sec.energy sec.industry sec.construction sec.services.venta sec.services.nonventa school.illit school.prim school.med school.high school.post.high popdens invest treat
1 Spain (Espana) 1955 2.354542 NA NA NA NA NA NA NA NA NA NA NA NA NA 0
1 Spain (Espana) 1956 2.480149 NA NA NA NA NA NA NA NA NA NA NA NA NA 0
1 Spain (Espana) 1957 2.603613 NA NA NA NA NA NA NA NA NA NA NA NA NA 0
1 Spain (Espana) 1958 2.637104 NA NA NA NA NA NA NA NA NA NA NA NA NA 0
1 Spain (Espana) 1959 2.669880 NA NA NA NA NA NA NA NA NA NA NA NA NA 0
1 Spain (Espana) 1960 2.869966 NA NA NA NA NA NA NA NA NA NA NA NA NA 0 
out_basque <- gsynth(gdpcap ~ treat, data = basque_treat, index = c("regionname","year"), force = "two-way",
                  CV = TRUE, r = c(0, 5), se = TRUE,
                  inference = "parametric", nboots = 1000,
                  parallel = FALSE, )

Cross-validating ...
 r = 0; sigma2 = 0.15833; IC = -1.31080; PC = 0.14556; MSPE = 0.02963
 r = 1; sigma2 = 0.02499; IC = -2.64303; PC = 0.04627; MSPE = 0.00994
 r = 2; sigma2 = 0.00985; IC = -3.07772; PC = 0.02745; MSPE = 0.00755*
 r = 3; sigma2 = 0.00581; IC = -3.12683; PC = 0.02166; MSPE = 0.00981
 r = 4; sigma2 = 0.00395; IC = -3.05355; PC = 0.01843; MSPE = 0.00329
 r = 5; sigma2 = 0.00256; IC = -3.04564; PC = 0.01435; MSPE = 0.00260

 r* = 5


Simulating errors .............
Bootstrapping ...
..........

Let’s check the results

plot(out_basque)+
  theme(plot.title = element_text(size = 12))


plot(out_basque, type = "counterfactual", raw = "all")+
  theme(plot.title = element_text(size = 12))

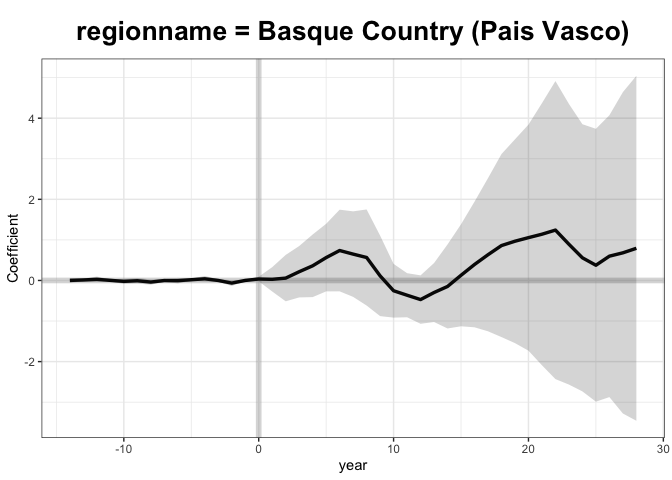
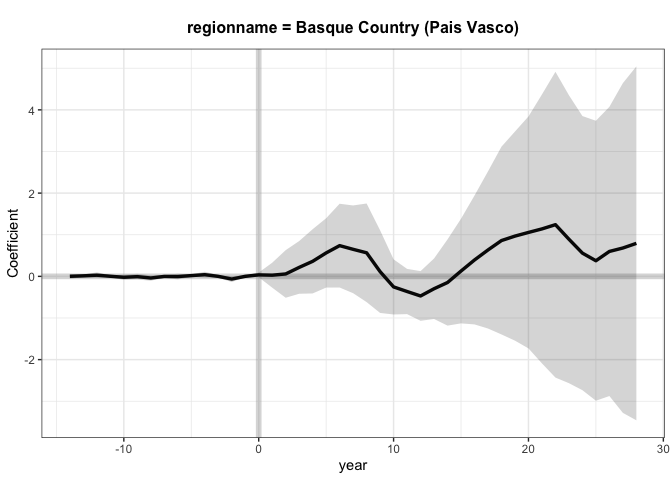
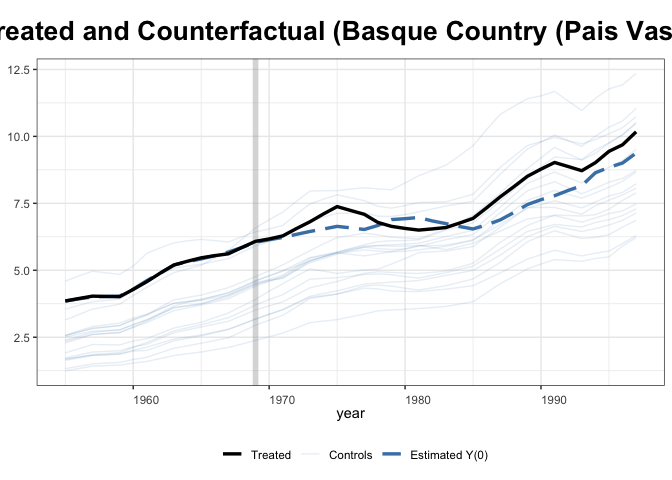
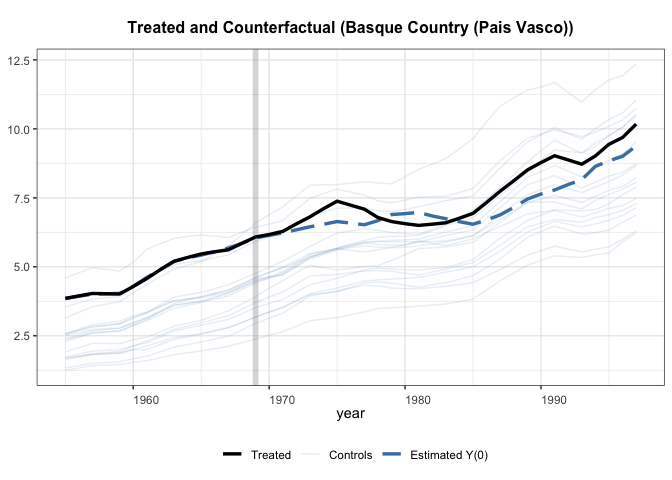
Interesting that this method lands on a slightly different estimate than the previous paper. I think that this is due to some missing covariates. It appears that gsynth doesn’t handle missing data too well, which is ok.

Thoughts

I think that a combination of Bayesian Hierarchical modeling with structural timeseries modeling could get somewhere close to the method, and take advantage of specifying knowns, group effects, etc. But the method is neat and a good way to do some quick analysis.

Abadie, Alberto, Alexis Diamond, and Jens Hainmueller. 2011a. “Synth: An R Package for Synthetic Control Methods in Comparative Case Studies.” Journal of Statistical Software 42 (13): 1–17. http://www.jstatsoft.org/v42/i13/.

———. 2011b. “Synth: An r Package for Synthetic Control Methods in Comparative Case Studies.” Journal of Statistical Software, Articles 42 (13): 1–17. https://doi.org/10.18637/jss.v042.i13.

Xu, Yiqing, and Licheng Liu. 2018. Gsynth: Generalized Synthetic Control Method. https://CRAN.R-project.org/package=gsynth.


Citation

BibTex citation:

@online{dewitt2018
author = {Michael E. DeWitt},
title = {Replicating gsynth},
date = 2018-10-29,
url = {https://michaeldewittjr.com/articles/2018-10-28-replicating-gsynth},
langid = {en}
}

For attribution, please cite this work as:

Michael E. DeWitt. 2018. "Replicating gsynth." October 29, 2018. https://michaeldewittjr.com/articles/2018-10-28-replicating-gsynth