• Home
• Contact
• Selected works
• Newsfeed
• About
• Search

This post is completely inspired by @mjskay ’s very interesting analysis/ critique of a New York Times linear extrapolation of when the United States would reach the critical proportion for vaccination. The New York Times has made some amazing graphics during the pandemic, but their analyses have been pretty spotty. Between this linear extrapolation of vaccination rates and their SIRs for third and fourth waves, they really need to put some additional thought into the more math heavy type work.

Matt uses Bayesian Structural Time Series implemented in the bsts package(which I really like) in order to make a more nuanced analysis. Additionally, because we know that the percent vaccinated is monotonically increasing and bounded between 0 and 1, we can make some transforms to our data.

North Carolina

I along with some work colleauges have been maintaining a package called nccovid (available at remotes::install_github("conedatascience/nccovid)) which allows for ready access to North Carolina COVID-19 related data. This does not represent the views of my employer.

Data Prep

First I am going to pull in the needed packages:

library(tidyverse)
library(lubridate)
library(ggdist)
library(tidybayes)
library(bsts)
library(patchwork)
library(tidyverse)
library(posterior)
theme_set(theme_ggdist())

And now we can pull in the North Carolina data:

dat <- nccovid::get_vaccinations()

nc_oa <- dat[,.(people_partial_vax = sum(people_partial_vax, na.rm = TRUE),
                                         population = sum(population, na.rm = TRUE)), by = "date"] %>%
  .[,vax:=people_partial_vax/population] %>%
  .[order(date)]

It’s good to plot these data just to make sure they “feel” right.

nc_oa %>%
  ggplot(aes(date, vax))+
  geom_line()+
  labs(
    title = "Cumulative Percent of North Carolinians Vaccinated",
    caption = "Data: North Carolina Department of Health and Human Services\nAnalysis: @medewittjr",
    y = "Percent Vaccinated"
  )+
  scale_y_continuous(labels = scales::percent)+
  geom_smooth(method = "lm", color = "red",alpha = .1, lty = "dashed")

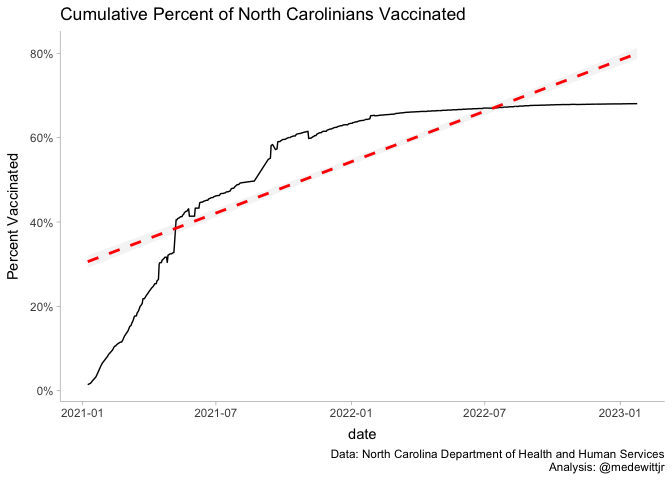
So we can see that linear fit for North Carolina likely isn’t valid, at least not in the last few weeks. Regardless, we have out data for the next steps of the analysis.

Data Transformation

As I mentioned earlier and a critical point of this analysis is that we know a few things about vaccinations. Firstly, vaccinations are non-reversible and are thus monotonically increasing (e.g., they can only increase). Additionally, depending on the definition you take, the percentage of the population vaccinated with a first dose is bound between 0 and 1.

With these features in mind, we can use a logit transform on our vaccinations and then fit that on our data.

nc_log_diff <- nc_oa %>%
  group_by(people_partial_vax) %>%
  mutate(id = row_number()) %>%
  filter(id == min(id)) %>%
  dplyr::select(-id) %>%
  ungroup() %>%
  mutate(log_diff_vax = c(NA, log(diff(qlogis(vax))))) %>%
  slice(-1)

Now we can fit the model using the priors that Matt used.

fit = with(nc_log_diff, bsts(log_diff_vax,
  state.specification = list() %>%
    AddSemilocalLinearTrend(log_diff_vax,
      level.sigma.prior = SdPrior(0.5, 1),
      slope.mean.prior = NormalPrior(0,0.5),
      initial.level.prior = NormalPrior(0,0.5),
      initial.slope.prior = NormalPrior(0,0.5),
      slope.sigma.prior = SdPrior(0.5, 1),
      slope.ar1.prior = Ar1CoefficientPrior(0, 0.5)
    ) %>%
    AddSeasonal(log_diff_vax, 7,
      sigma.prior = SdPrior(0.5, 1)
    ),
  prior = SdPrior(0.5, 1),
  niter = 40000,
  seed = 336
))

=-=-=-=-= Iteration 0 Sat Jan 13 15:59:50 2024 =-=-=-=-=
=-=-=-=-= Iteration 4000 Sat Jan 13 16:00:10 2024 =-=-=-=-=
=-=-=-=-= Iteration 8000 Sat Jan 13 16:00:30 2024 =-=-=-=-=
=-=-=-=-= Iteration 12000 Sat Jan 13 16:00:50 2024 =-=-=-=-=
=-=-=-=-= Iteration 16000 Sat Jan 13 16:01:10 2024 =-=-=-=-=
=-=-=-=-= Iteration 20000 Sat Jan 13 16:01:30 2024 =-=-=-=-=
=-=-=-=-= Iteration 24000 Sat Jan 13 16:01:49 2024 =-=-=-=-=
=-=-=-=-= Iteration 28000 Sat Jan 13 16:02:09 2024 =-=-=-=-=
=-=-=-=-= Iteration 32000 Sat Jan 13 16:02:30 2024 =-=-=-=-=
=-=-=-=-= Iteration 36000 Sat Jan 13 16:02:50 2024 =-=-=-=-=

Diagnostics (that I did not know could be leveraged from posterior. just a really great package).

draws <- as_draws(do.call(cbind, fit[startsWith(names(fit), "trend") | startsWith(names(fit), "sigma")]))
summary(draws, median, mad, quantile2, default_convergence_measures()) %>%
  knitr::kable(digits = 3)

All of the Gelman-Rubin statistics look good as well as the effective sample sizes, so I’m happy with what I see. However, it is always good to visualize the outputs as well:

bayesplot::mcmc_trace(draws)

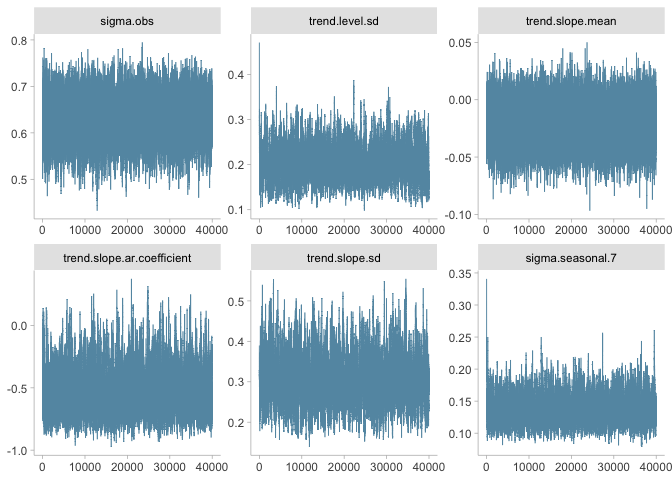
Trace plots look pretty good as well.

Predictions

Now we can predict out with our model for 180 days.

forecast_days <- 180

fits <- nc_log_diff %>%
  add_draws(colSums(aperm(fit$state.contributions, c(2, 1, 3))))

predictions <- nc_log_diff %$%
  tibble(date = max(date) + days(1:forecast_days)) %>%
  add_draws(predict(fit, horizon = forecast_days)$distribution, value = "log_diff_vax")

Now we need to convert our predictions back into percentages:

pred_vax = predictions %>%
  group_by(.draw) %>%
  mutate(
    vax = plogis(cumsum(c(
      qlogis(tail(nc_log_diff$vax, 1)) + exp(log_diff_vax[[1]]),
      exp(log_diff_vax[-1])
    )))
  )

Results

Now we can visualize the outputs. We see that there is a high degree of uncertainty regarding what proportion of the population will likely be vaccinated in the coming 180 days.

widths = c(.5, .8, .95)
pred_vax %>%
  ggplot(aes(date, vax)) +
  stat_lineribbon(.width = widths, color = "#08519c") +
  scale_fill_brewer()+
  geom_line(data = nc_oa, size = 1)+
  labs(
    title = "Percent vaccinated (at least partially vaccinated)",
    subtitle = "For the State of North Carolina",
    y = NULL,
    x = NULL
  )+
  scale_y_continuous(limits = c(0,1), labels = scales::percent_format())

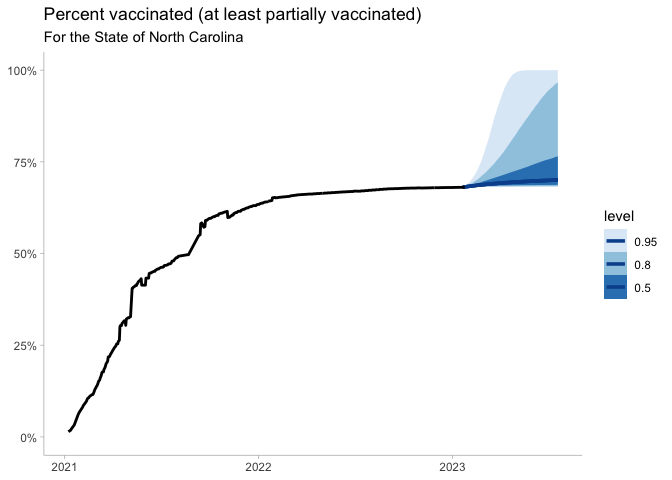
The next big question is what will be our likely vaccine coverage. If we want to target 80% of the population vaccinated, which is aggressive, but needed if $R0$ of SARS-CoV-2 is close to 4-4.5 and the vaccine effectiveness is between 90-95%.

prob <- pred_vax %>%
  group_by(date) %>%
  summarise(prob_vax_gt_x = mean(vax > .80)) %>%
  ggplot(aes(date, prob_vax_gt_x)) +
  geom_line(color = "#08519c", size = 1) +
  theme_ggdist() +
  geom_hline(yintercept = 0.5, alpha = 0.25) +
  scale_y_continuous(limits = c(0,1), labels = scales::percent_format()) +
  labs(
    subtitle = "Pr(Percent vaccinated > 80%)",
    y = NULL,
    x = NULL
  )

prob

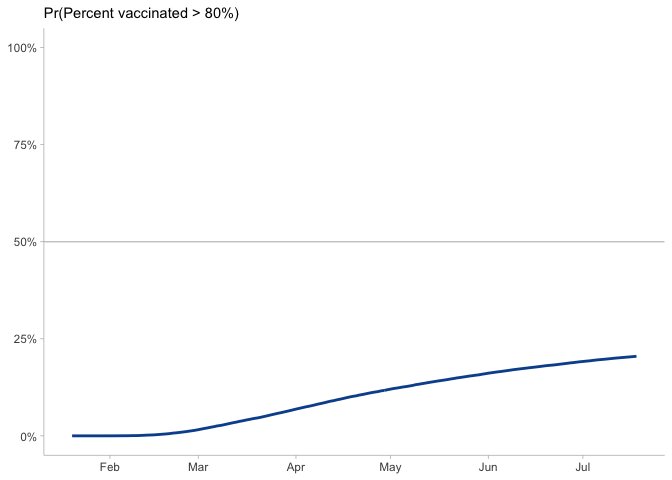
Sadly, it looks like that is a low probability outcome.

What about a county?

Just for fun I want to run through a single North Carolina County and see if there is any difference.

# Oddly one day showed a decrease...government records....
forsyth_log_diff <- dat[county=="Forsyth",c("county",
                                            "people_partial_vax",
                                            "population",
                                            "date")] %>%
  .[,vax:=people_partial_vax/population] %>%
  group_by(people_partial_vax) %>%
  mutate(id = row_number()) %>%
  filter(id == min(id)) %>%
  dplyr::select(-id) %>%
  ungroup() %>%
  mutate(log_diff_vax = c(NA, log(diff(qlogis(vax))))) %>%
  filter(!is.na(log_diff_vax)) %>%
  slice(-1)

fit = with(forsyth_log_diff, bsts(log_diff_vax,
  state.specification = list() %>%
    AddSemilocalLinearTrend(log_diff_vax,
      level.sigma.prior = SdPrior(0.5, 1),
      slope.mean.prior = NormalPrior(0,0.5),
      initial.level.prior = NormalPrior(0,0.5),
      initial.slope.prior = NormalPrior(0,0.5),
      slope.sigma.prior = SdPrior(0.5, 1),
      slope.ar1.prior = Ar1CoefficientPrior(0, 0.5)
    ) %>%
    AddSeasonal(log_diff_vax, 7,
      sigma.prior = SdPrior(0.5, 1)
    ),
  prior = SdPrior(0.5, 1),
  niter = 40000,
  seed = 336
))

=-=-=-=-= Iteration 0 Sat Jan 13 16:03:50 2024 =-=-=-=-=
=-=-=-=-= Iteration 4000 Sat Jan 13 16:04:10 2024 =-=-=-=-=
=-=-=-=-= Iteration 8000 Sat Jan 13 16:04:29 2024 =-=-=-=-=
=-=-=-=-= Iteration 12000 Sat Jan 13 16:04:49 2024 =-=-=-=-=
=-=-=-=-= Iteration 16000 Sat Jan 13 16:05:09 2024 =-=-=-=-=
=-=-=-=-= Iteration 20000 Sat Jan 13 16:05:29 2024 =-=-=-=-=
=-=-=-=-= Iteration 24000 Sat Jan 13 16:05:48 2024 =-=-=-=-=
=-=-=-=-= Iteration 28000 Sat Jan 13 16:06:07 2024 =-=-=-=-=
=-=-=-=-= Iteration 32000 Sat Jan 13 16:06:26 2024 =-=-=-=-=
=-=-=-=-= Iteration 36000 Sat Jan 13 16:06:45 2024 =-=-=-=-=

fits <- forsyth_log_diff %>%
  add_draws(colSums(aperm(fit$state.contributions, c(2, 1, 3))))

predictions <- forsyth_log_diff %$%
  tibble(date = max(date) + days(1:forecast_days)) %>%
  add_draws(predict(fit, horizon = forecast_days)$distribution, value = "log_diff_vax")

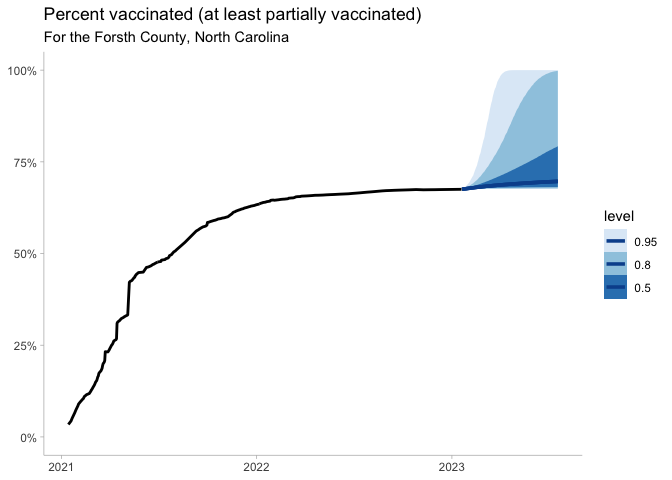
pred_vax = predictions %>%
  group_by(.draw) %>%
  mutate(
    vax = plogis(cumsum(c(
      qlogis(tail(forsyth_log_diff$vax, 1)) + exp(log_diff_vax[[1]]),
      exp(log_diff_vax[-1])
    )))
  )

pred_vax %>%
  ggplot(aes(date, vax)) +
  stat_lineribbon(.width = widths, color = "#08519c") +
  scale_fill_brewer()+
  geom_line(data = forsyth_log_diff, size = 1)+
  labs(
    title = "Percent vaccinated (at least partially vaccinated)",
    subtitle = "For the Forsth County, North Carolina",
    y = NULL,
    x = NULL
  )+
  scale_y_continuous(limits = c(0,1), labels = scales::percent_format())

pred_vax %>%
  group_by(date) %>%
  summarise(prob_vax_gt_x = mean(vax > .80)) %>%
  ggplot(aes(date, prob_vax_gt_x)) +
  geom_line(color = "#08519c", size = 1) +
  theme_ggdist() +
  geom_hline(yintercept = 0.5, alpha = 0.25) +
  scale_y_continuous(limits = c(0,1), labels = scales::percent_format()) +
  labs(
    title = "Pr(Percent vaccinated > 80%)",
    subtitle = "For Forsyth County, North Carolina",
    y = NULL,
    x = NULL
  )

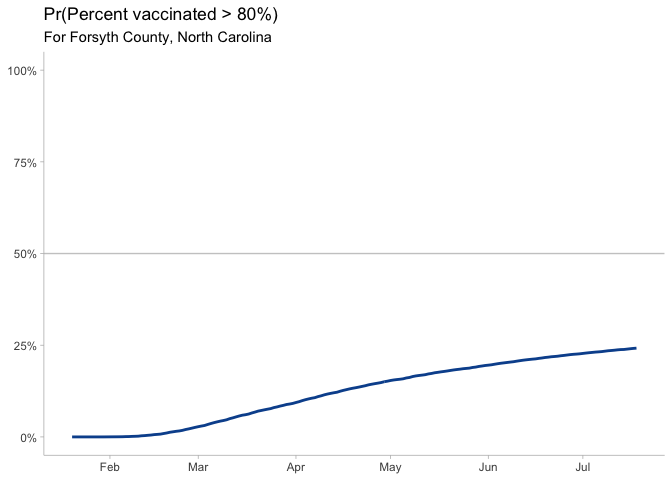
Hmm, not too much better

knitr::include_graphics("notbad.gif")

Citation

BibTex citation:

@online{dewitt2021
author = {Michael E. DeWitt},
title = {Time to Vaccinate},
date = 2021-05-07,
url = {https://michaeldewittjr.com/articles/2021-05-07-time-to-vaccinate},
langid = {en}
}

For attribution, please cite this work as:

Michael E. DeWitt. 2021. "Time to Vaccinate." May 7, 2021. https://michaeldewittjr.com/articles/2021-05-07-time-to-vaccinate